Disclaimer
Copyright (c) Arturo San Emeterio Campos 2000. All rights reserved.
Permission is granted to make verbatim copies of this document for private
use only.
Download
Download the whole article zipped. It
includes the C source code as well as compiled binaries for Dos.
Table of contents
This article is about ppmc, a lossless compression algorithm which achieves compression higher than some commercial products. This articles shows in deep how to implement ppmc using hash tables and linked lists. Different versions of it are explained, ppmc with lazy exclusions, ppmc with full exclusions (slower than the previous but achieving more compression) and a tricky version of ppmc, ppmc order-3 hashed, the only ppm implementation which is practical in the compression/speed/memory tradeoff. Ppmc can be used as an standalone compressor or with other algorithms like lzp for coding of the literals [14], due to his high compression level. You are encouraged to see the results in speed and compression to see if this is the algorithm that you need. Understanding ppmc is the key to understand ppmz, the state of art in text compression [3]. The explanations follow the code that is released along with the article. This article presupposes a theory which is explained in my article about finite context modeling [6].
The article is distributed in the following way:
Some historical review is done. After that, some terminology
is explained. First I talk about
cumulative
probabilities, linked lists, the probability
of the escape code, and hash
tables for contexts. These sections describe all the algorithms and
code used for managing the model and encoder which are later needed. Then
we see how to put everything together. Some global
variables and data structures are discussed, the initialization and
some other code is explained too. The next section explains more about
the code and the functions for
coding, decoding and updating. Then the algorithm is commented from the
lowest
order till order-4, once there it's only a matter
of implementing the code explained before. Due to the fact that the data
structures and functions from one context don't depend on others, the idea
is to have order-(-1) working before starting implementing order-0, and
so on. This makes programming very easy, and it helps finding bugs. My
implementation uses bytes as symbols as its goal is to compress files.
At first all the functions will be explained for lazy exclusion. Then there's
a section about how much memory
needs every data structure and every order, and how it's managed. After
this there's a section about full exclusion
which shows how to make ppmc with full exclusions, from the code already
done. Also I talk about a fast order-3 hashed
ppmc implementation, which is as fast as order-2 but achieving more compression
(not as much as real order-3 of course). At the end of the article you
may find the
results of different
ppmc implementations, in both compression and speed. The algorithm is explained
in the way I found easier to understand, the basic order-0 is explained,
then the concept "context" is used order-1. We make order-2 from order-1
using linked lists for probabilities, and a hash table for contexts. Based
on order-2 we make both order-3 and order-4, which are a natural extension,
using a hash table and linked lists for storing the contexts. Every concept
is based on the previous, and thus I don't add difficulties to the already
complex process of learning.
Ppmc, history review and data structures
used
Prediction by Partial Matching is the Markovian model which achieves higher compression. Markovian models are those who have the Markov property: the probability of the current symbol only depends on the symbols which appeared before. Due to the increasing power and memory available in today's machines some ppm implementations are practical. Some others are not like the actual state of art in lossless text compression: ppmz2 by Charles Bloom. Other states of art are CTW [13] and the switching schemes of Paul Volf (though nowadays they are still hardly know). The main programming difficulty of ppm models is the data structure that holds all the contexts to be used. The first data structure used was the context trie in [3] or [4]. The context trie uses a linked list for every order. In every node there's a byte and its count, and pointer to the next element in a linked list containing the rest of the bytes under that context. For traversing the structure there's a pointer to the next higher order, obviously at the root of the tree you can find order-0. Optionally (for higher speed) there's another pointer to the next lower order (used when escaping). This data structure is used for bounded (limited) orders of a length of 5 or so. But for unbounded orders (that is, of non previously chosen length), which are very long, this is not satisfactory due to the high memory usage.
The patricia tree and, mainly, the suffix tree are a solution to this problem. The suffix tree is used in ppmd [5]. However suffix trees are more difficult to implement than other solutions.
In [8] hash tables were used, I've not checked this paper though. Thus I'll explain how to implement ppmc with hash tables without following it. The ideas exposed in this article are based on the implementation of ppmz by Malcolm Taylor. Hash tables are easy to learn, so they fit quite well this article. Moreover they are the appropriate structure structure for ppmz, and another of the goals of this article is to learn the base of ppmz. Just as a little overview of ppmc with hash tables, every context has its own hash table and linked lists where the bytes (or symbols) and counts are stored, then it's only a matter to read the count of a symbol, compute probabilities and code it. All the theory behind ppm was explained in "Finite context modeling" [6] so it's recommended to read it before this one. Along with this article, I've released my implementation of ppmc in C. I'll not try to focus much on it, because this would cause problems to the reader interested in implementing it in other language, anyway I'll follow it.
Ppm was invented by John Cleary and Ian Witten back in 1984. The original paper [9], talked about ppma and ppmb. The suffix letter ('a' or 'b') denotes the escape code used in the algorithm, however the rest of the algorithm is roughly the same. In the book "Text compression" [2] all of them were explained. Ppmc was presented by Alistair Moffat in [7]. In the paper by Moffat also ppmc' was presented, which is ppmc but using lazy exclusion. Other variants such as ppmd, ppm* or ppmz fall outside the scope of this article, however I'll probably talk about them too in a near future. The difference between ppmc and ppma or ppmb are only the probability computation for the escape code.
As we saw in [6] ppm variants are finite context models. Practical implementations don't use blending. They use escape codes instead. They fallback to lower orders when needed. That is, they start at the highest order initialized, if the byte is present they code it under the current context, otherwise they emit an escape code, fallback to (use) a lower context and try to code the byte under that context. The last context (order-(-1)) contains all the bytes, so we'll surely find it there if it wasn't present in higher orders. We code the probability with arithmetic coding, or any variant (like in the case of the source, the range coder [11]). Once the byte is coded, it's only a matter of updating the probability of the symbol which we have just coded. As we are going to see later, ppmc uses update exclusions, which does not only make it faster but also achieves slightly better compression. How to implement update exclusions is explained in the section Global variables.
If we are using escape codes, when we are in a given context we exclude lower orders from probability computing, because we just take in account the probabilities of current one, that's ppmc using lazy exclusions. If we exclude symbols which have appeared in higher orders from the probability computation that's called full exclusion.
Once we have the probabilities, we code them optimally
(respect to the entropy) with arithmetic coding, which is explained in
[10] and [2]. The range coder,
a variant of it is explained in [11] and the original
source code can be found in [12].
Some terminology and a
brief look to a model
This is only a brief look to some terms which may
cause problems, for more theory you are encouraged to read [6]
Context are the symbols or symbol which come before or after current one
(in ppmc only before). Order-n refers to n bytes of context. In a given
message a symbol can appear k times, this is its frequency. From there
the model computes its probability, which in ppmc comes in the form of
probability/total_probability, like 1/4. Ppmc rescales the frequencies,
so they are called counts instead. If we have the message "bacabac" the
ppmc model would look like the following if we don't take the escape code
in account (bytes in order of appearance).
| Order-3:
Context: "bac" list: 'a'-1 Context: "aca" list: 'b'-1 Context: "cab" list: 'a'-1 Context: "aba" list: 'c'-1 |
Order-2:
Context: "ba" list: 'c'-2 Context: "ac" list: 'a'-1 Context: "ca" list: 'b'-1 Context: "ab" list: 'a'-1 |
| Order-1:
Context: "b" list: 'a'-2 Context: "a" list: 'c'-2 'b'-1 Context: "c" list: 'a'-1 |
Order-0:
Context: "" list: 'b'-2 'a'-3 'c'-2 |
Under order-0 the probabilities are: 'a' 3/7, 'b' 2/7 and 'c' 2/7. For
more examples, see [6].
Cumulative probabilities
and how to manage them
Arithmetic coding optimally encodes a symbol given
its probability (optimal compared with the entropy, which has been proven
to be the minimum, read [1]). In arithmetic coding
we distribute the symbols in a probability line (between 0 and 1), then
to encode a symbol we need to know its cumulative probability and its probability.
The cumulative probability of the first symbol in the probability line
is 0. For any other symbol its cumulative probability is the sum of all
the probabilities of the symbols before it. We do so to assign ranges of
this probability line to every symbol, and that thus we can latter know
which is the encoder symbol, knowing only its cumulative probability.
| Symbol: | a | b | c | d | e |
| Count: | 2 | 3 | 0 | 1 | 2 |
| Probability: | 2/8 | 3/8 | 0/8 | 1/8 | 2/8 |
| Cumulative probability: | 0 (0.0) | 2 (0.25) | 5 (0.625) | 5 (0.625) | 6 ( 0,75) |
| Range: | [0 , 0.25) | [0.25 , 0.625) | [0.625 , 0.625) | [0.625 , 0.75) | [0.75 , 1) |
In the example above we have in first file the count of the byte, in some cases that could be the frequency. But as we'll see later ppmc uses renormalization, and thus it's the count instead. The second has the probability of the byte, note that 8 is the total count (the sum of all the counts). Then the cumulative probability is computed for every symbol as explained above. The last file has the theorical range assigned for this symbol. The symbol 'c' has an invalid range, however it's supposed that we'll never try to code it (in a real implementation of ppmc instead we would have coded an escape code). When implementing ppmc you don't need to compute the range for the symbols. Arithmetic coding only needs the count of the symbol, its cumulative probability and the total count (the sum of all the counts).
Though in my implementation and some other you can find other terms like probability referring to the count, the terms used above are the correct ones. Probability is used to refer to count just because count/total_count is the probability. The total count is also called maximum cumulative probability. Expect different names and misuses not only in my article but also in others, but don't forget the correct names.
In the implementation we'll keep tables (or linked lists for orders higher than 1) with the count of every byte. Based on this we have to compute the cumulative probabilities and maximum cumulative probability. We don't need all the cumulative probabilities, only the cumulative probability for the symbol that we want to code (the symbol that we are modeling now). From the explanation of how to compute the cumulative probabilities we can derive the following pseudo code:
This is the code used for order-0 and order-1, where a byte's probability can be found in counts_table[byte]. The complexity of this code is O(K) where K is the position of the byte in the table. It's worth mentioning that this is the greatest overhead of simple a arithmetic coding implementation, and also an important part (in time execution) of ppmc. Once the code above is executed and assuming that we have the maximum cumulative probability (as it will be seen later, that's stored in every context) we can code the symbol. In this example counts_table[] stores the counts of the symbols under the current order (which is assumed for simplicity to be 0).
With this information the arithmetic coder can compute
its range:
[ symbol_cumulative_probability / maximum_cumulative_probability ,
( symbol_cumulative_probability + symbol_probability ) / maximum_cumulative_probability
)
And encode the symbol. This is not the point of this article, however
note that arithmetic coding compresses best symbols with higher count because
it can use all the range to represent this number, for example in the table
above 'b' ( [0.25 , 0.625) ) can be represented with 0.25, 0.3, 0.4, 0.5,
0.6, 0.6249999, etc.
When decoding you need the maximum cumulative probability
(which we have assumed to be already know), and the arithmetic decoder
will return a cumulative probability. This cumulative probability distinguishes
the symbol coded. We have to search it in our table, and then update the
arithmetic coding state. As stated before we only store the counts, so
we have to compute the cumulative probability on the fly to search our
symbol. Let's say that we have the same table as in the previous example:
| Symbol: | a | b | c | d | e |
| Count: | 2 | 3 | 0 | 1 | 2 |
| Cumulative probability: | 0 | 2 | 5 | 5 | 6 |
We need to read till the next byte of the coded one. For example with a cumulative probability of 4 we know that the encoded byte was 'b' (because 4 lands in its range) however to know so we have to read till the 'c', whose cumulative probability is 5, so we can be sure that the decoded byte is the right one, the previous. We'll compare the decoded cumulative probability with the one computed on the fly, when it's higher we can be sure that the previous byte was the encoded one. But what about if both have the same value? in this case we can't be sure. Let's say we have encoded a 'd', the cumulative probability is 5, but when decoding if we stop comparing when they are the same, we would decode a 'c' which is wrong. If we however stop only when the computed one is greater, we would stop in the 'e' and thus correctly decode a 'd' (the previous symbol). We have to do so because we have to care about both the lower and higher bound. Having all the previous in mind we do the following decoding routine:
In this code we compute the cumulative probability (on_the_fly_cumulative_probability) only for the current symbol in each step, because we don't need the cumulative probability of symbols which are in positions after the byte to decode. Note that this code is the same as for any simple order-0 arithmetic coding implementation. And that they use a table where the entry of a byte is the value of the byte itself (the count of 'byte' is in count_table[byte]). Due to this at the end of this routine we decide that the decoded byte is counter-1, because counter is the current one and counter-1 is the previous, note that the symbols are in order. In linked lists this will be different, but we'll see this later. We already know the decoded byte thus we know its probability and cumulative probability, so we can update the state of the arithmetic coder.
To save some space in higher order tables we may
want to reduce the size of the count. For lower orders we can use double words
(32 bits) but for higher orders is better to use only a byte (8 bits).
Every time the count is incremented we have to check that it isn't the
maximum, if it is we have to halve all the counts. We divide all of them
by a factor of 2. This is called renormalization or rescaling. In the case
of linked lists we don't want that the count of a byte is 0, so when this
happens, we change its value to 1. Renormalization does not only save space
but also increases compression a little bit. That is because the probabilities
of text change within a file, thus giving more importance to newer frequencies
improve compression, because it reflects the changes in the source (the
probabilities of the file).
Escape method C, how to
compute and use it
The escape method C was already discussed at [6] and can be also found in [2]. I'll recall the example table, where a symbol ('c') had a count of 0. In ppmc we'll suppose that all the orders are initially empty (unless the order-(-1)), when we want to code in any order that is totally empty we just don't code anything. But what happens if there's only one symbol or just a few? how can we transmit to the decoder that the byte that we want to finally decode is not present in this table? For doing this we use the escape code. Both compressor and decompressor assign the same probability to the escape code. There are different methods for estimating the escape probability. Ppmc uses the escape method called 'C' (and that's why it's called ppmc) Method C assigns a count to the escape code equal to the number of different symbols that have appeared under this context. For practical issues we assume that the escape code is the last one. We also have to take care of its probability when coding. Let's see the table that we are using for examples, how it is without using escape code and with it:
|
|
As I have said before, in every context we'll store the maximum cumulative probability. Also we'll store the number of different bytes (which in my implementation is called defined_bytes). Due to this I call the maximum cumulative probability "max_cump", but because we also have to take in account the code space of the escape code, I have another variable called "total_cump", which is the maximum cumulative probability plus the count of the escape code (which for method C is the number of different bytes), this is the value which must be using when calling the decoding functions.
But how does the escape code affect to coding and
decoding? In encoding before trying to make the cumulative probability
of the current byte and coding it, we have to check that it exists or that
it has a non zero probability. If everything is ok then we can code it,
otherwise the context is present but the byte is not, so we have to code
an escape code. We know the probability (which comes from the count) of
the escape code, it's simply the number of defined bytes in that context.
But what about its cumulative probability? Due to how the cumulative probabilities
are computed and also due to the fact that we assume the escape code to
be the last symbol, the cumulative probability of the escape code is the
maximum cumulative probability.
"max_cump" is the total count before adding it the escape code's count.
If you have a look at the table above, you'll see that max_cump is 8, and
that the escape code's cumulative probability is also 8. Taking all those
facts in account we use the following pseudo code:
In the case of decoding we have to check if the coded symbol is an escape code, we do so based on its cumulative probability (which is stored) otherwise decode as usual:
Linked lists for the counts
of the bytes
All the algorithms used above work only if we have
all the symbols in order and in a table where the entry of 'byte' is in
count_table[byte]. This is a good idea for order-0 and order-1 where the
tables may take up to 1,024 and 262,144 bytes respectively (in case we
use double words (32 bits) for the count). But this is not acceptable for
order-2 which would need 67,108,864 bytes to hold all the tables (256*256*256*4).
For higher orders the amount of memory is not available nowadays. Moreover
due to the fact that there are less high context than lower ones, most
of the entries are not used. The solution to both problems is using a linked
list for storing the counts. A linked list is made of different elements,
every element has its own value and a pointer to the next element. We store
on it the count, and also the byte. In the case of tables (which in fact
were hash tables with direct addressing) we knew the value of a byte by
its entry, now we don't, so we have to store the value of the byte too.
The last element in the linked list, has a pointer with a value of 0, meaning
that it's the last one. Using linked list we can dynamically allocate memory
only for the entries that we are going to use. Let's have a look at our
table of example, which now is a linked lists:
|
||||||||||||||||||||||||||||
As you can see in linked list form, there's no entry for 'c' because it has not appeared, in our example the linked list is sorted, but in the implementation you'll find them in order of appearance, the first that appeared will be the first in the linked list. In my implementation I kept a buffer where new nodes were allocated. Once this buffer was full, another one was allocated. The pointers to all the allocated buffers were stored in one array. When compression or decompression is done, all the allocated buffers are freed. |
|
The data structure of a linked list in C is the following:
struct _byte_and_freq
{
unsigned char byte; //The value of the byte
unsigned char freq; //The count of the byte
struct _byte_and_freq *next; //Pointer to the next
node in the linked list
}
In a linked list new nodes are stored at the end.
For example if we had to put 'c' in the list, we should read the linked
list till the end, once at the end, allocate memory for this new buffer.
Then put in the node of 'e' a pointer to this new location. The new element
should have the following values: byte 'c', count 1, pointer 0. Its pointer
is 0 because now it is the last element in the linked list. In our implementation
we don't need to delete nodes of the linked list, so we make it even easier.
Coding
and decoding with linked lists
For coding we need to know if a given byte is present in the linked list, if it is we can code it. To check if it's present, we have to read the whole linked list till we find it or reach the end. When implementing this we'll already have a pointer to the first element, so we we'll assume so. Checking all the elements is only a matter of reading current one, if it's not the one we are looking for, get the pointer to the next, and so on, till we hit the end of the linked list. The pseudo code is like the following:
For the readers who don't know the C language, pointer_ll->byte, means accessing the value called 'byte' in the data structure addressed by the pointer 'pointer_ll'. We also need to know the cumulative probability of the byte, to do so we need the code explained before. We have to read all the elements till the byte. Both the code needed for searching a symbol and checking if it's present and the code for making the cumulative probability do the same. So why not merging them? In the same loop we have to check if the byte is present or not and compute its cumulative probability, for the case that it is present. Later we'll have to update the count of this byte, and because we want to avoid having to read the linked list again, we store the pointer in a global variable. But if the byte is not present when we update we'll have to add a new pointer to the end of the linked list, for that case we store a pointer to the last element.
Updating the count of a byte with tables was done just by accessing its entry. For linked list we don't know its position beforehand, so we have to search it in the linked list, when found, update its count. But in fact we know its position: when we code the symbol we need to read the linked list, so if we keep a pointer to it, we'll not need to read the whole linked list again. As I've explained before, the linked list nodes are allocated in a big buffer, to avoid having to call the functions of memory allocation for every new node. When updating we have to check whatever the encoder emitted an escape code or a byte. One could think that we could check if the pointer of the node (o2_ll_node) is 0, in that case this is the last element and thus the end of the linked list was reached. But this is false. Imagine that we found the byte but it was in the last position, in that case the pointer is also 0. The solution is to check if the byte is the same, that unambiguously distinguishes between the two cases. In all the examples before we assumed that max_cump and defined_bytes were stored in the context, now we have to update them aswell. As long as we have coded the byte (or an escape) with the code above, the following pseudo code would update the model.
|
|
|
|
| Symbol: | e | b | a | d |
| Count: | 2 | 3 | 2 | 1 |
| Cumulative probability: | 0 | 2 | 5 | 7 |
However as I've explained before we don't need to actually build this table, only as much as needed. Linked lists are a little bit more difficult to manage than tables for decoding, mainly in the search (when we have to get the previous symbol). Also another problem is in updating: we can't ensure that the pointer (in case of an escape code) points to the last element, because the decoding routine doesn't need to read the linked list to identify an escape code. The latter problem has no other solution that reading the whole linked list when updating and an escape code was emitted. However the second has two solutions. Remember that we have to read till the next byte of the one to decode? at first glance one could think that like we did with the tables we have to read till the next symbol. But then how do we get the previous? in that case we should have a variable which always has the last byte in the linked list. Fortunately there's a better solution. Why do why need to read the next element? because we need to know the upper bound of the cumulative probability. For tables the fastest (and thus it was used) way is reading the next element's cumulative probability. However for linked lists its better to sum to the current cumulative probability the count of the byte. That way we also have the upper bound. Then we can check if we have to stop. And the node pointer will point to the byte that we have to decode.
To avoid problems when using linked lists for cumulative
probabilities, we don't allow any count to be 0. When renormalizing we
check if it's 0, in this case we put the value of 1.
Hash tables are arrays used to store and find items. A hash table which allows direct addressing has one entry for every item. This is obviously very memory consuming if the number of items is big. In the cases where direct addressing is not possible, we use chaining for resolving collisions (collisions are two or more contexts sharing the same hash entry). The item of the hash table instead is a pointer to a linked list. This linked list contains the different contexts. The value of the context itself is stored for checking. Also we store a pointer to the linked list with the bytes and counts. One hash table is used for every order. Hash tables and linked list for contexts are only used for orders above 2.
Let's say we have a hash table for order-1 which has only two entries. And we have a hash function which maps the items in the following way: 'a','b','c' entry 1. 'd', 'e', 'f' entry 2. After having stored the contexts 'e','b','d','a','c' it would look like the following:
Hash table:
| Hash entry | Value |
| 1 | Pointer to linked list, element 'b' |
| 2 | Pointer to linked list, element 'e' |
Big memory buffer for linked lists:
|
|
|
|
|
The structure of a context
node in a linked list is:
struct context
{
struct context *next; //Next context in the linked
list (corresponding to this hash entry)
unsigned long order4321; //Order-4-3-2-1 (or order-3-2-1
for order-3), that's the value of the context
struct _byte_and_freq *prob; //Pointer to linked
lists containing bytes and counts of this context
unsigned int max_cump; //Maximum cumulative probability
in this context
unsigned int defined_bytes; //The number of bytes
in this context
};
Note that we could reduce the space needed by using a byte (unsigned char) instead of a double word (unsigned int or unsigned long, 32 bits) for the number of bytes in the context, however then we should add 1 every time we read this value (to make 0 represent 1 instead, and so on). I decided to not make the code more difficult to read. Thus this is not implemented in my ppmc implementation. See the section of fast order-3 hashed for another example.
The code for managing the linked lists with contexts is the same as the code for the counts and bytes. For contexts, the value that makes every element different is "order4321" instead of "byte". When we want to read the counts of a context, we have to read the pointer in its hash entry. If this entry is empty, the context was not initialized yet, so we fallback to the next lower order without emitting escape code. Then use this pointer to search current context in the linked list of contexts, if it's not present we also have to fallback without escape code. In case we found it, we'll read the pointer to the linked list with the bytes and counts. Because we already know the maximum cumulative probability, and the number of defined bytes, we can code the byte as explained before. But let's have a look at the implementation.
The first function called by both encoding and decoding functions is "ppmc_get_totf_order3". Thus this is the function which is going to read the linked list with contexts and ensure that the current one is present. The first thing is to do the hash key. After that we need to have the context in a variable, in that case because it's order-3, an unsigned long is ok, if we want higher orders, say 6, we would have order-4-3-2-1 in an unsigned long, and the rest, order-6-5 in another one. We'll use this variable for comparing while searching for the context.
The first thing to check is that current entry in the hash table for this order is initialized. The table is initialized to 0, so if current entry is 0, it's not initialized, otherwise it would have a pointer. If it isn't we can be sure that there's no context in this entry, so we have to abort. "ppmc_get_totf_order3" unlike functions for lower orders returns a value. I decided to make it return a 0 in case that the hash entry was not initialized or the context not present, and a 1 in case it is.
Now we get the pointer from the entry to the linked list with contexts and store it in "cntxt_node". And now we have to read all the linked list till we find current context, if we reach the end before we find it, the context is not present and thus we have to return a 0, so the encoding or decoding functions know that they can't code in this order.
Once we know that the context is present we have to return the total cumulative probability. Note that this is different for full exclusions.
Now encoding and decoding functions would be able to do their job. After that we have to update the count of current byte. Now we rely on the fact that "o3_cntxt" and "full_o3_cntxt" are initialized. While updating four different cases can happen:
In the first case we have to create a new node in the linked list of context in the current hash entry. The way we allocate memory is explained in the section about memory management. Then we have to initialize this node, and also put pointer to this new node in the hash table. After that we have to put a new symbol in the linked list with probabilities, see the section about linked lists for that matter. The code is like the following:
If the byte was coded under current context we just have to update its count. We can assume that "o3_ll_node" and "o3_context" are initialized, so the code becomes as easy as that:
Once the two first cases have been discarded, it may happen that an escape occurred or that In the third case an escape code has to be coded because current context was not present in the linked list of context. Because the case of an uninitialized hash entry was already discarded we can be sure that there's at least one context in the linked list of current hash entry for contexts. The way to know which one of those cases is to check the context in the pointer, if it's the same as the current one we can be sure that an escape was coded, because in that case the context existed, and we already discarded the case that the byte was coded under this context.
Otherwise we know that it's pointing to the last element in the linked list of contexts, because when looking for current context, it wasn't found so it reached the end of the linked list, and also updated the variable "o3_context". But however we know that the context was present (because there was at least 1 symbol). Thus the only thing to do is to create a new node in the linked list for bytes and probabilities as shown in the section of linked lists.
In the fourth case the context was not present in
the linked list corresponding to this hash entry. What we do is reading
till the end of the linked list for context (though I think this is not
really needed) and then put a new node as explained above,
with the only difference that the pointer is stored in the last element
in the linked list instead in the hash entry of the current order.
In some cases (unbounded length contexts) we need to have the whole file loaded in a buffer. However in this implementation the maximum context that we need is order-4 (but we could very easily extent this to order-8, at the cost of speed and memory, though). Thus we store the contexts in another way. Because C has some restrictions, we store the contexts in unsigned chars. One unsigned char for every byte, order-1 is stored in o1_byte, order-2 is stored in o2_byte and so on. Thus is we have the context "ther", o1_byte = 'r', o2_byte = 'e', o3_byte = 'h', o4_byte = 't'. If the next byte to code is an 'e', after coding it, the context would be: o1_byte = 'e', o2_byte = 'r', o3_byte = 'e', o4_byte = 'h'. In assembly language we could store the whole order-4 in a double word (32 bits), and then just read a byte for order-1 and so on.
In high orders (3,4) we need to have the hash entry and also the full context so we can compare it when finding the context in the linked list. In the case of order-3 we have "o3_cntxt" which contains the hash key used to index in the order-3 hash table. And "full_o3_cntxt" which contains all the order-3. In the previous example "o3_cntxt" depends on the hash function, and "full_o3_cntxt" = "ere". For order-4 only the number changes, that is "o4_cntxt" instead of "o3_cntxt".
For making the code easier to read, the arithmetic coding routines (range coder) are called with the same variables. They are: total_cump with the total cumulative probability, symb_cump symbol cumulative probability, and symb_prob the probability (count) of the symbol.
Ppmc uses update exclusion. That is we only update in the order where the byte was coded and higher ones. In my implementation I use a variable called "coded_in_order" whose value is where the byte was coded. If the byte was coded under order 3 the value of "coded_in_order" will be 3. If it was coded in order-(-1) its value will be 0 though. It has a 0 value to update the right orders. The code in C used for updating is this:
switch(coded_in_order)
{
case 0: ppmc_update_order0();
case 1: ppmc_update_order1();
case 2: ppmc_update_order2();
case 3: ppmc_update_order3();
case 4: ppmc_update_order4();
default: break;
};
Which means that if the value of coded_in_order is 0, all the functions for updating will be called. And if it's 3 then only the functions for order-3 and order-4 will be called.
For memory usage I use "ppmc_out_of_memory". If it's 0 then there's still memory available. If it's 1 there's not. Every function which needs to allocate memory aborts in the case its value is 1. Once we have a problem allocating memory, this variable is set to 1. At the end of the loop we check this variable, and in case it's 0 we flush the model. This is explained in the section of memory management.
Before starting to model and code the input we have to reinitialize the model. The main job is to allocate the memory needed for the hash tables and linked lists. Moreover tables from low orders, like order-0 and order-1 must be cleared, that is all the counts must have a value of 0. The hash tables of high orders must be cleared too, that is we must put a value of 0 in the offsets stored. Apart from that we have to care about initialising the context variables by reading from the input, updating the variables and writing directly to the output. Once this is done we can start with the main loop. Have a look at the source if you have any question about these steps.
Now we'll see how to implement every order, don't try doing order-0 until order-(-1) doesn't work, and so on. But before going in that matter we'll see which functions uses every order and what they do.
Note that there are some variables different for
every order which are pointers to linked list of contexts or bytes, and
which are initialized in a function, and then in another function are used.
One example is a pointer to the linked list with bytes of the order-2 which
is initialized
(to whatever it has to be) in the function of encoding,
and which is used later while updating. So it's not a good idea to modify
these kind of variables between those functions.
Functions nomenclature
and use
Every order uses different functions to manage their data structures. For increasing readability of the code they follow some guidelines, all functions that do the same have the same name (the only difference is in the number of the order). They do the same things, in the sense that they are called in the same way and achieve the same goals, though most of them use different code.
When decoding we need to know the maximum cumulative probability for being able to decode the input, so in this case, and also while encoding, the first function called is "ppmc_get_totf_order2". Which stands for: get the total frequency, in fact frequency and probability are different things, as I explained before, unfortunately I perpetuated this error, but I suggest you to not do so. However the term maximum cumulative is already used for referring to the sum of the counts of all the bytes so not using this term for different things can help to avoid misunderstandings. The function "ppmc_get_totf_order2" does nothing else than returning in "total_cump" the maximum cumulative probability of the current context. As explained in the section about the escape method this can be quickly done by adding the number of defined bytes in the context (the count of the escape code) and the maximum cumulative probability. Also remember that "total_cump", "symb_cump" and "symb_prob" are used as the parameters for arithmetic coding. (in the case of my source a range coder)
The function "ppmc_code_byte_order2" (the number '2' should be changed if we want the function for another order) codes the byte in the current symbol if it's present, in that case it returns a 1. It may happen that under this order, the current context is not present, in that case it doesn't code anything, and returns a 0. It could happen too that in current order the context was present but the byte we have to code wasn't, so an escape code must be coded and the function will return a 0. From this you can see that the main loop of the compressor just have to call the encoding routine for highest order, and call the next lower one in case it returns a 0, or stop when it returns a 1.
Another job of the ppmc model is to update the count of the current symbol, this is done by calling "ppmc_update_order2". This function returns nothing, and the main loop doesn't have to check whatever it worked or not. At least not till the updating is done. In higher orders the decoder uses a different function for updating "ppmc_update_dec_order2", because some care should be taken with the linked lists.
When the count of a byte gets too big for the date type used for storing it, renormalization (halving counts) must be done. The function "ppmc_renormalize_order2" does this. It's called from the routine of updating.
For decompression, "ppmc_decode_order2" is called.
It just returns "-1" if the byte was not decoded (because current context
didn't exist or it was an escape code) otherwise it returns the byte in
the variable "byte". The main loop of the decoder would check if the returned
value is "-1" in that case it would try to decode in a lower order.
Every order uses its own functions and the only work of the main part is calling them, this makes the code easier to read and to expand. The first thing is writing to the output file the length of the input file, that way the decoder will know when to stop. After that we start initializing the model and coder:
Once this is done we start the main loop, we read a
byte from the input till there are no more bytes. Then we try to code in
the highest order and if failed, in a lower one. In the worst case we'll
code the byte in order-1. After that we have to do the updating, keeping
in mind that we do update exclusion, that is we only update the same order
as the byte was coded in, and higher ones. Then we update the context variables
and check for memory problems. The code is like the following:
The order-(-1) in the code is called "ordern1" meaning negative one. As we saw in the article about finite context modeling order-(-1) is the lowest order whose only job is to be able to code all the symbols that may appear in the input. Order-1 is not used for achieving compression, so it's never updated. Because it must give a non-zero count to all the symbols but it's not updated, we use a flat probability distribution. That is every symbol has the same probability. For matters of the implementation every symbol has a 1 count. The alphabet has all the bytes, from 0-255 in the same positions, and an special code, the 256 which is used for flushing the model when running out of memory. Thus we have that the probability of every symbol in the order-(-1) table is 1/257.
At first we could think about having a table with
the counts and cumulative probabilities of every symbol, but having a look
at those values we realize that this is not needed.
| Symbol: | 0 | 1 | 2 | 3 | n | 256 |
| Count: | 1 | 1 | 1 | 1 | 1 | 1 |
| Cumulative probability: | 0 | 1 | 2 | 3 | n | 256 |
We see that the cumulative probability of a given byte is the value of the byte itself. We can take profit of this fact and avoid using any table. So the first function to implement "ppmc_get_prob_ordern1" is quite easy, it just has to assign a 257 for the maximum cumulative probability (no need of escape code), 1 to the probability, and the value of the byte to the cumulative probability.
The function for returning the byte of a given cumulative probability is very easy too, the byte is the value of the cumulative probability.
Because this order has the only job of being able
to code all symbols, it's not update, so we don't need to care about that
matter.
Order-0 and order-1 are not memory hungry, so we
can store them in tables. If you have already implemented any arithmetic
coder, you surely know how does order-0 works. Given this, order-1 is only
a little modification: in order-0 we keep the probabilities in this table
"order0_array[]" and access it directly (that is the probability for "byte"
is in "order0_array[byte]"), order-1 uses instead "order1_array[o1_byte][byte]".
The only difference from an usual implementation is the escape code. Now
it's only a matter of implementing it having in mind the differences pointed
in the section about Cumulative probabilities.
Order-2 needs more memory than order-1, the probabilities can't be stored on tables, because it would take too much memory. Thus the probabilities are stored in linked lists. Order-2 has 2^16 = 65536 contexts, we can afford to put the contexts in a table. Like a hash table with direct addressing, obviously the hash key is just the order-2, for the context "there" the hash key would be "re", thus we would find the context in "order2_array['re']". Due to the fact that in every entry we only have one context, we don't need to store the context nor use linked lists for contexts, so the data structure used is similar to the one used for higher orders, but with these differences.
struct o2_context
{
struct _byte_and_freq *prob; //Pointer to linked
lists containing bytes and counts of this context
unsigned int max_cump; //Maximum cumulative probability
in this context
unsigned int defined_bytes; //The number of bytes
in this context
};
Putting all together we have that the maximum cumulative probability of order-2 with a context like "which" is in:
The hash key as already explained is very simple,
and the only thing it does is putting two bytes, the order-1 and order-2
bytes, in a variable, which will be used to access the array for order-2.
#define ppmc_order2_hash_key(k,j) ((k)+(j<<8))
Now it could happen that the context hasn't been created yet, so we have to check it. As explained before once a byte in a linked list in created, it's never deleted, so just by checking the number of defined bytes we can see if the context has been already created. If the count is 0 it hasn't, so we have to return without coding anything.
Now we use the code explained in the section of Coding and decoding with linked lists and code an escape code or the byte depending on if the byte wasn't present or it was.
The next function to implement is "ppmc_update_order2", because we saved in "o2_ll_node" the pointer to the linked list, we don't need to read the linked list again, and thus we can update the order as explained in Coding and decoding with linked lists.
Decoding is not much more difficult just follow the
explanations at
Coding
and decoding with linked lists, and remember to check first if context
exists. The function for updating while decoding can't rely on the fact
that "o2_ll_node" points to the last element, so it has to read all the
linked lists, till the end and put new nodes there. This happens when the
byte was not coded under order-2. Check the code if you have any question.
We can't use a table for contexts in order-3 because it would be too big, it would require 16,777,216 entries and every entry would take around 12 bytes. We can't afford that, so instead we use linked lists for storing contexts. Read Hash tables for contexts.
While encoding or decoding the first function called
is "ppmc_get_totf_order3", this one is responsible for checking if current
context is present, and also updates the variable "o3_context" (or
"o4_context" for order-4), it contains a pointer to the entry, and thus
the functions now are as in order-2 but instead of "order2_array[o2_cntxt]"
we use "o3_context". Apart from some special care while updating, all
the functions are the same, so you only have to change that and you already
have order-3 working. Both order-3 and order-4 are managed in the same
way. So do one, and copy the code for the next one.
Memory
requirements and management
The basic data structures are the following:
| struct _byte_and_freq{
unsigned char byte; unsigned char freq; struct _byte_and_freq *next; }; |
struct context{
struct context *next; unsigned long order4321; struct _byte_and_freq *prob; unsigned int max_cump; unsigned int defined_bytes; }; |
struct context_o2{
struct _byte_and_freq *prob; unsigned int max_cump; unsigned int defined_bytes; }; |
Thus they take:
| Structure | Unaligned | Aligned |
| _byte_and_freq | 6 bytes | 8 bytes |
| context | 20 bytes | 20 bytes |
| context_o2 | 12 bytes | 12 bytes |
The static memory of the program, memory which is
not allocated while the program runs takes is the showed in the table.
This is the memory that the programs just need to start.
| Order-0 | 256 |
| Order-1 | 66048 |
| Order-2 | 786432 |
| Order-3 | 262144 |
| Order-4 | 262144 |
| Bytes pool | 1000000 |
| Context pool | 1000000 |
| Total | 3377024 |
Order-(-1) doesn't need any array. Order-0 uses an array with the count (8 bits) for every byte. Order-1 uses the same table but 256 times, thus 256*256, moreover we need two arrays for every byte (256 entries thus) for "defined_bytes" and "max_cump". Order-2 has a hash table with direct addressing, because we'll address two bytes (order-2 context) we need 256*256=65,536 entries. Every entry uses the data structure context_o2, thus it takes 65536*12=786,432 bytes. Order-3 instead has a hash table with pointers to contexts, it has 65,536 entries and is a pointer which (in my implementation) takes 4 bytes, 65536*4=262,144. Order-4 uses exactly the same. The pool for bytes and contexts take 2,000,000 bytes, we'll explain now why.
We have to allocate memory for every new element in the linked list. It wouldn't be a good idea to call the functions for doing so every time. Also there's another fact that we should be aware of while thinking about how to allocate memory, an element in the linked list is never deleted. Due to these facts the solution that I chose for my implementation was having a big buffer, and put there new nodes there. Keeping track of the next position and the last one with pointers. Once this buffer is filled we have to allocate a new one. Given this solution, there's still two parameters to choose, the length of the buffer, and the maximum number of buffers to allocate. I decided to give them a value of 1,000,000 and 100 respectively. We can choose to have another value, the length of new buffers, that way you could allocate a very bug buffer at the start (suited to your needs) and allocating less memory for the new buffers, expecting to not need a lot. This could save some memory, but should be tuned. Though in my implementation I have both definitions, they have the same value.
Again having code clarity in mind I chose to have two buffers, one for the linked lists containing bytes and probabilities, and another for the contexts. The code is the same and only the nomenclature (names assigned) for the variables is different, thus instead of "_bytes_pool_elements" there's "_context_pool_elements". The variables used for this code are the following ones:
The defined values follow too. We get the length of any buffer by multiplying it by its size, so the size of a buffer for contexts is 50,000*20=1,000,000. I decided to make every buffer one mega long, it seemed like a reasonable value, because it was big enough to not need to allocate another buffer soon, and that it was not so big that it couldn't be allocated it today's computers.
If we allocate a new element the steps to follow are clear: first let the routine use the pointer at "_context_pool" for the new entry, second increment the pointer and then check that this is not the last entry, if its we should allocate another buffer. We can do another paranoid check, that is checking that we still have any entry free in the table where we store the pointers to the big buffers. We could avoid it by being sure that we have enough buffers (which probably is the case).
After allocating memory for the new buffer, we put its value in the table, and compute the value of the end of the buffer, obviously it's the pointer plus the maximum number of entries (in case of assembly you first should multiply this value by the length of every entry). Then we increment the index tot the table with pointers to the big buffers, which will be used when freeing memory.
When the compressing process is done, or when we have to flush the encoder, we have to free all the buffers. At the start of the program we cleared all the entries of the table with pointers to the big buffers, so we have to check if it's non zero, in case it isn't, then it's a pointer, and we have to free it. In C we only need to know the pointer of the buffer to free it, in other programming languages you might need storing additional information.
The flushing routine has to ensure that everything (variables, tables and buffers) is like if it was just initialized. First we have to free all the memory. Then clear all the tables for all orders, that is all the probabilities of order-0 and order-1 set to zero, and all the pointers of higher orders to 0. Then the big buffers must be allocated again. In my implementation I had to set the count of the current byte in order-0 to 1 too. Next we have to emit the flush code. We have to visit each context and if there's any probability, emit an escape code in this order. Once we reach order-(-1) we can emit the flush code, which in my implementation is done with:
The decoder checks the symbol decoded under order-(-1)
before writing it in the output, in case it's a flush code, it has to flush
its model, no matter if it still has memory (this could happen if the file
was compressed in a computer with more memory). In my code I do even another
check, in case that "ppmc_out_of_memory" = 1, but we didn't decode a flush
code, that means that compressor had more memory than decompressor, in
that case we just can't decompress the rest of the file correctly, because
we can't keep track of changes in the model (new nodes), so we can only
exit. To check this at the end of the loop we check if the variable "expected_flush"=1
(it's initialized to 0) in case it's we exit. After that we check if we
run out of memory. If we do, we set "expected_flush" to 1, and thus if
next time we don't decode a flush code, it means that we have to exit,
which will be done by the check explained before.
How to implement the
fast order-3 hashed version
With hash tables we can do a trick which in most of the cases is of not use, but in this one resulted in something which works quite well. The trick is simply not resolving hash collisions. Thus let different contexts share the same entry. We only need to implement order-2, once we have it working we change the hash key for order-2 for the hash key of order-3:
#define ppmc_order2_hash_key(k,j) ((k)+(j<<8))
#define ppmc_order3_hash_size 65536
#define ppmc_order3_hash_key(k,j,i) ((k)+(j<<7)+(i<<11))
& ppmc_order4_hash_size-1
If you are not used to C '&' means the AND mask, in the case of hash keys we use it for erasing the high bits that we don't use (because we restricted the length of the hash table). The '<<' are left shifts.
Now we just have to change the main part to use order-3
instead of order-2, we only have to use the variable "o3_byte" too. And
it's all done. Now in the same hash entry there will be different contexts
sharing the same probability list. This doesn't produce bad results, instead
it works better than order-2, though of course it works worse than real
order-3. However if we extent the same trick for order-4 the results are
bad. These are the results for book2. (time for compression in kbyps)
| Order | Bpb | Time (c) |
| 2 | 2.8629 | 246.696 |
| 3h | 2.3713 | 237.134 |
| 3 | 2.2849 | 205.995 |
| 4h | 2.4934 | 146.716 |
It's worth mentioning that order-3h uses almost as much memory as order-2, because they use the same hash tables. Order-3 can take a little bit more of memory in linked lists for bytes and probabilities. The difference from order-2 and order-3h in compression is big while in speed and memory usage is very little! This happens because though different contexts are sharing the same probability list, they aren't quite different or because there are just a few contexts in the same entry. In the other hand in order-4 a lot of contexts share the same entry, with may be different probabilities, so at the end we get worse compression, because the same context (hash entry in that case) gives a probability distribution which doesn't reflect current file.
The differences in speed can be explained too. They all come from insertion and updating of nodes in the list of bytes and their counts. 3h or 4h have to create and update more nodes, and while coding and decoding there are more symbols in the cumulative probabilities, so the process is slower.
Order-3h is a ppmc implementation well suited for real world compression because it only takes a little bit more of speed and memory than order-2, but achieves 0.5bpb more, which ranks it in a good position.
If
you wonder how this works, let's put an example. Let's say we have a binary
message, that is, the alphabet only contains 1 and 0. And our hash key
looks like the following:
#define ppmc_order3_hash_key(k,j,i) ((k)+(j<<1)+(i<<1))
& 11 (binary)
And we have a context like "101". If we apply it the hash key the result
is (all the values are in binary): 1+00+10=11. 11 would be the hash entry
of context "101". But this however is also the hash entry of "011" (using
hash key:) 1+10+00=11. So at the end we have that both contexts "101" and
"011" share the same entry. In their entry there's the probability list
for 0 and 1. And there we would store the probabilities of the two contexts.
In our implementation of ppmc the contexts which share the same entry have
for sure the same order-1 byte, so more or less they have the same probability
distribution, and thus it doesn't suffer much. In fact the error in prediction
in book2 results only in 0.0864 bpb.
If we analyse it, see that we have 2^3 = 8 possible
input values which are mapped to 2^2 = 4 hash entries, thus every entry
is share by 8/4 = context. In our hash key for ppmc we have 2^24 = 16,777,216
contexts which are mapped (that is, we assign them a position in the hash
table) to 2^16 = 65,536 (this is the number of entries in the hash
table). Thus we have that in ppmc order-3h every entry holds 256 different
contexts. 256 different probability distributions in every list, however
the impact in compression is little because due to our hash key the contexts
which share the same entry are similar.
#define ppmc_order3_hash_key(k,j,i) ((k)+(j<<7)+(i<<11))
& ppmc_order4_hash_size-1
In our hash key "k" is "o1_byte" and the hash key as worst modify the
highest bit, but the rest remain untouched, so we know for sure that all
the contexts that share the same hash entry have the first seven bits of
order-1 the same.
Another thing which I had to check was using a classic hash key (used for example in lzp [14]) instead of the current one. Instead of '+' a '^' (xor)
Using ^ Using + File Bpb Kbyps c Kbyps d File Bpb Kbyps c Kbyps d book1 2.5531 218.5143 214.8418 book1 2.5415 236.7239 221.6721 book2 2.3997 237.1344 213.9184 book2 2.3859 241.8208 227.4374 geo 4.8769 86.9565 82.6446 geo 4.9209 90.9091 86.9565 obj2 3.0717 182.5980 162.8576 obj2 3.0635 191.2931 175.9338 progc 2.6109 182.4308 182.4308 progc 2.6010 182.4308 182.4308 news 2.8417 186.2531 167.2981 news 2.8194 203.2762 186.2531 Average 3.0590 182.3145 170.6652 Average 3.0554 191.0756 180.1139
The use of xor instead of adding resulted in worse compression
and speed for all the files except geo, which is a list of floating point
numbers. The hash key for order-3 works better with "+" for text. The test
files come from
[15].
Adding full exclusion to
the already done functions
Full exclusion is when we exclude from probability
computation symbols which appeared in orders which we already used. Obviously
if in an order there's a symbol but we instead emit an escape code, because
it wasn't the symbol to code, it will not be coded, so we shouldn't assign
it any probability. Let's say we have a message with the following probabilities:
| Order-3
'a'-2 'b'-4 'c'-0 escape-3 |
Order-2
'a'-6 'b'-7 'c'-1 escape-3 |
And we want to code 'c'. In order-3 we don't find it, so we emit an escape code with a probability of 3/9. Then in order-2 we find it and emit it with a probability of 1/16 (4 bits). As you see in order-2 we allocate probability space for 'a' and 'b', though they appeared in order-3 and we didn't select them, therefore they are not the byte to code. So we decide to use full exclusion instead of lazy exclusion (which excludes lower orders) then if we exclude 'a' and 'b', the escape code has a probability of 1 (the scheme C assigns it a value equal to the number of defined bytes in the context, which now is only 'c') then we code 'c' with a probability of 1/2 (1 bit).
For full exclusion we use a table with an entry for every symbol (in the case bytes this means a table with 256 entries, which is acceptable), this table is accessed like "excluded[byte]", and has a value of 0 if it's not excluded, and a value of 1 if it is. At the start of loop (every itineration, of course) we put all the values to 0, because no order has been visited yet. If a context emits an escape code, we update this table, by putting the value of the bytes in that order to 1. That way they'll be excluded in lower orders. Then when computing probabilities, we don't take in account bytes excluded. For making the coding easier to read, I decided to use some new variables: "exc_total_cump", "exc_defined_bytes" and "exc_max_cump" which are self-explanatory. In the case of order-(-1) (ordern1 in the code) I chose not to use full exclusions, because order-(-1) is hardly used. Also if you implement full exclusions, you have to be careful about a problem that can arise.
The change over previous versions is mainly done in the function "ppmc_get_totf_order2", which has to exclude from the probability computation the excluded bytes, comparing its value in the "excluded" table.
We start by clearing both maximum cumulative probability and defined bytes, then we read till the end of the linked lists, and check if current byte is excluded, if it isn't we can update the values. When the end of the linked list is reached (the pointer "next" is 0) we break the loop, and then we compute the maximum cumulative probability.
The function for coding would first call "ppmc_get_totf_order2", but now it could happen that due to exclusion there was no byte defined in the context, thus we have to check it and return a value meaning that we didn't code the byte.
After that we have to compute its probability, the code used is the modification of the code used with lazy exclusions, in that case we just have to car about excluded bytes:
Then it's only a matter of coding the byte. But in the case an escape occurs we do not only have to emit it, but we also have to update the "excluded" table. As explained before we have to read all the linked list and then put to 1 the value of the bytes present under that context:
There's room for optimization. If we code the byte under this context we read the linked list twice, and if we don't we read it three times, which can be of course improved. It's possible to make the symbol cumulative probability while making the maximum cumulative probability, and thus we would avoid reading the linked list again when coding the symbol. Even we should be able to not read the linked list again the third time, in that case we should update the table "excluded" while computing the maximum cumulative probability, of course we should update the count after having read it. I haven't tested the idea nor the code, but with both optimizations the code would look like the following:
In this code we exclude all the symbols which appear in current order, if an escape occurs that was what we had to do, if we code a byte, it doesn't matter because then we are not going to use "excluded". Note we can't apply this optimization to the decoding functions, because we first need to know the maximum cumulative probability for decoding, then we have to read the linked list for finding the symbol.
The function for decoding starts by doing the same as the encoding function, that is making "exc_max_cump", and then checking that there's at least one byte defined in the order. In case an escape occurs we do the same as when coding. The routine for decoding the symbol is a modification of the one used for lazy exclusions, which doesn't take in account excluded bytes.
I leave as an exercise to the reader adapting the functions for order-0 and order-1, if you find any problem have a look at the source code.
Warning: the updating function assumes that if the byte was not coded under order-2 (or higher) it didn't exist in the linked list, and that it has the pointer "o2_ll_node" initialized to the last element in the linked list due to the search done during the encoding process. This is however not true. It may happen that all the characters are excluded (due to the fact that they appeared in higher orders) thus "get_totf" would return a 0 in the variable "exc_defined_bytes". The encoding function would check it and abort (obviously if there's no byte in the context we can't code anything). Thus the pointer to the linked list is not initialized. The solution to this problem is just reading till the end of the linked list while updating. Note that this is not needed in the highest order, because none of the symbols is excluded because it's the higher. Therefore in my code I haven't done this change in the function for updating of order-4. So be careful if you want to put another higher order. Use the code for order-3 which takes this in account and has linked list for probabilities and contexts.
The literature tends to say that full exclusion is
excluding the symbols which appeared in higher orders, but this is not
true for ppmz, which uses LOE (Local Order Estimation) for selecting the
best order for current symbol. I.e: let's say the maximum order is 8, but
LOE chooses to try to encode current symbol in order-5, an escape occurs,
and then LOE selects order-3, now we'll use full exclusion, but we don't
exclude all the bytes of higher orders, because we don't know them (at
encoding time we do, but while decoding we won't), it could even happen
that our byte is present there. We only exclude the orders which we have
seen which in this case is only order-5.
Compression and speed
results of the different implementations
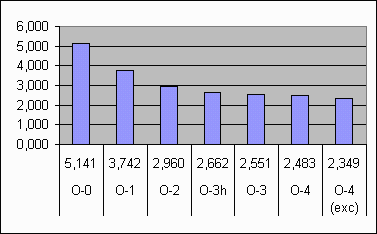
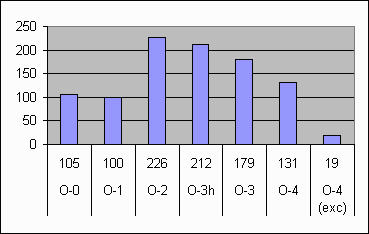
A little comparison between different orders and implementations is shown in the graphics. O-3h is order-3 hashed, and o-4 (exc) is ppmc order-4 with full exclusions. The compression is measured in bpb and the speed in kbyps.

|

|
The results which follow correspond to the three different implementations, ppmc with lazy exclusion, ppmc with full exclusion and ppmc order-3 hashed. Note that the implementation with full exclusions could be faster. These are results for the Calgary Corpus, and at the end you can also see the results for the large Canterbury corpus [16].
Full results: Ppmc lazy exclusion, order-4 File Bpb Kbyps c Kbyps d book1 2.4757 136.9617 118.1796 book2 2.1989 150.3210 126.6680 bib 2.0030 139.9831 123.4259 geo 5.3678 45.6621 42.3729 news 2.8141 107.7190 94.2877 obj1 4.0171 95.4545 77.7778 obj2 2.7300 91.2990 79.8110 paper1 2.5560 139.8309 106.2715 paper2 2.5191 134.3654 113.8373 pic 1.3235 190.5656 146.0821 progc 2.5625 121.6205 105.6178 progl 1.8593 163.9959 131.1967 progp 1.8602 151.9442 128.5682 trans 1.6749 167.7681 139.8068 Average 2.5687 131.2494 109.5645 Ppmc order-3 hashed (lazy exclusion) File Bpb Kbyps c Kbyps d book1 2.5415 236.7239 221.6721 book2 2.3859 241.8208 227.4374 bib 2.2053 229.5723 229.5723 geo 4.9209 90.9091 86.9565 news 2.8194 203.2762 186.2531 obj1 4.0532 190.9091 131.2500 obj2 3.0635 191.2931 175.9338 paper1 2.6161 189.7705 189.7705 paper2 2.5515 210.1613 215.6918 pic 1.3430 327.5735 294.8162 progc 2.6010 182.4308 182.4308 progl 1.9551 257.7079 267.2526 progp 1.9208 227.9164 227.9164 trans 1.9003 236.5961 236.5961 Average 2.6341 215.4758 205.2535 Ppmc full exclusion, order-4 File Bpb Kbyps c Kbyps d book1 2.2723 21.1874 22.5584 book2 1.9947 22.5509 22.9227 bib 1.8522 22.4630 23.2361 geo 4.7744 7.4906 9.0580 news 2.3807 20.8546 17.2488 obj1 3.8140 8.3004 10.6061 obj2 2.5281 16.7498 18.6700 paper1 2.3264 21.0023 21.0856 paper2 2.3028 18.6704 20.6977 pic 1.2678 20.1848 20.0075 progc 2.3511 20.2701 19.7708 progl 1.7235 25.3187 23.4280 progp 1.7267 22.1865 20.3002 trans 1.5737 23.3601 21.8138 Average 2.3492 19.3278 19.3860 Ppmc full exclusion, order-4 File Bpb Kbyps c Kbyps d bible.txt 1.7062 29.5428 28.9945 e.coli 1.9560 32.8449 31.6604 kjv.guten 1.6801 28.8764 28.3149 world192 1.6892 28.1551 27.9047 Average 1.7579 29.8548 29.2186
References
[1] Charles Bloom "Kraft Inequality", http://www.cbloom.com
(Compression : News Postings : Kraft Inequality)
[2] Bell, T.C., Cleary, J.G. and Witten, I.H. (1990)
"Text compression", Prentice Hall, Englewood Cliffs, NJ.
[3] Charles Bloom "Solving the Problems of Context
Modeling", http://www.cbloom.com
(ppmz.ps)
[4] Mark Nelson, Jean-Loup Gaily (1996) "The Data
Compression Book", M&T Books. Source available at Mark's page.
[5] Ppmd source code by Dmitry
Shkarin available via ftp1
or ftp2.
[6] Arturo Campos (1999) "Finite context modeling"
available at my home page.
[7] Moffat, A. (1988) "A note on the PPM data compression
algorithm," Research Report 88/7, Department of Computer Science, University
of Melbourne, Parkville, Victoria, Australia.
[8] Raita, T. and Teuhola, J. (1987) "Predictive
text compression by hashing." ACM conference on Information Retrieval,
New Orleans.
[9] Clearly, J.G. and Witten, I.H. (1984) "Data
compression using adaptative coding and partial string matching" IEEE Trans.
Communications, COM-32 (4), 396-402, April.
[10] Arturo Campos (1999) "Arithmetic coding"
available at my home page.
[11] Arturo Campos (1999) "Range coder" available
at my home page.
[12] Michael Schindler. Source code of the range
coder. Available via html.
[13] The Context-Tree Weighting Project. http://ei0.ei.ele.tue.nl/~frans/ResearchCTW.html
[14] Charles Bloom "LZP: a new data compression
algorithm", http://www.cbloom.com (lzp.ps)
[15] Calgary corpus set. ftp://ftp.cpsc.ucalgary.ca/pub/projects/text.compression.corpus
[16] large Canterbury corpus http://corpus.canterbury.ac.nz
Now you can use your ppmc implementation for an stand alone compressor of lossless files, or use it for lossless image compression, or using it for compressing the output of other compression algorithms (read next paragraph). However those are not the only uses of ppmc, you can use it for predicting and use it for an operative system where the reader needs to input text, or as a help for OCR [2]. If you want better compression than ppmc you should know that using an order above 4 with ppmc isn't worth because higher orders produce too much escape codes. For taking profit of the information that high orders provide you should have a look at other implementations like ppmd or ppmz. Fortunately ppmc with hash tables is the perfect base for ppmz [3] an state of art. I'll write an article about it, so keep an eye to my home page.
If you want to use ppmc for compressing the output of lzp (literals), you have to change update functions of higher orders, because currently they expect that coding is always done before updating. However in this case, a lot of literals are coded with lzp but have to be updated with ppmc too. For orders lowers than 2 there's no problem, but for order-2 and highers, we have to read till the end of the linked list of contexts or probabilities when we want to put a new element, or we have to read till the current one to update its count (variables like "o2_ll_node" are not initialized because the coding has not been done). Such changes are easy to do and are left as homework, in case you have any doubt email me.
If when implementing ppmc with full exclusions you find any bug, read the warning about updating. If still you can't find the bug, have a look at the code, or email me. This article took long to do, and thus I look forward for your comments about it, so please take the time to tell me what you think of it, just as I took the (long) time to write it.
I want to thank to Malcolm Taylor for letting me see
his ppmz code which used hash tables, unfortunately later he was too busy
to be able to answer my questions, which at the end I solved myself.
You can reach me via email at: arturo@arturocampos.com
See you in the next article!
This article comes from Arturo Campos home page at http://www.arturocampos.com Visit again soon for new and updated compression articles and software.